and
differently. That is 0 -> 1 is different from 1 --> 0. We call this model a dynamic process / Markov Transition process. To use a language of a real example, it can be stated like this:
A mechanism of transition to an authoritarian regime is different from transition to a democratic one.
Anyway, to show the model is a matrix form:
I began to pay attention to ``Dynamic Probit Models" when Epstein et al (2006) published a paper in American Journal of Political Science--``Democratic Transition." Here is the abstract:
Przeworski et al. (2000) challenge the key hypothesis in modernization theory: political regimes do not transition to democracy as per capita incomes rise, they argue. Rather, democratic transitions occur randomly, but once there, countries with higher levels of GDP per capita remain democratic. We retest the modernization hypothesis using new data, new techniques, and a three-way rather than dichotomous classification of regimes. Contrary to Przeworski et al. (2000) we find that the modernization hypothesis stands up well. We also find that partial democracies emerge as among the most important and least understood regime types.
However, what attracted my attention is that Epstein et al accuse Przeworksi et al of miscalculating the SE's of the dynamic Probit models. I must admit I get lost in Epstein et al 's presentation about the models. The math just did not ring the bell. But it turns out that the model is actually easy to fit.
I learned dynamic Probit models in 2002 from Professor Adam, Przeworksi at NYU. Back then I know every little about statistics. The only stats software I know is SPSS. Adam taught us how to do all the models in Przeworski et al. (2000) using LIMDEP. There is no way a SPSS user would catch up the learning of LIMDEP because LIMDEP is a programming language. SPSS is just a canned stats package. So I got lost in the class mostly because I was incapable of using LIMDEP. Well, the math was like Greek to me back then, too.
So I paid a visit to Adam last year (2007), hoping he can share me some sample code of how to fit dynamic Probit model. Actually, I was was hoping since I am good at another programming language, R, that I can know what the model is about this time.
Adam was not feeling well last year. I had to go to NYU three time to finally meet him. He did not give me any code. But he shared with me what he learned about dynamic Probit model recently.
A good professor teaches us how to do thing right. A great professor just shows you the direction.
The key is that the two processes are separated. Conditional on y(t-1), we will have two subsets: data[y(t-1)==1, ] and data[y(t-1)==0, ].
In short, we can fit two separate Probit models to get the same answer as the answer of the above big ugly matrix form. Here is the simple R code (you have to create ylag first):
# transition from 0 to 1
fit.01 <- glm(y ~ x, subset=ylag==0, family=binomial(link="probit"))
# transition from 1 to 0
fit.10 <- glm((1-y)~x, subset=ylag==1, family=binomial(link="probit"))
.gif)
.gif)
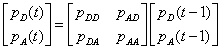




1 comment:
Interesting post: I'm getting here three years later. Now I myself am trying to replicate the results of this book and I am wondering whether you already did that. Do you have some R code for the dynamic probit and other models? Best, Antonio.
Post a Comment